Cylindrical Projections

简述球体的各类圆柱面投影方式

参考了 Cartographic Projection Procedures for the UNIX Environment—A User’s Manual 和 Wikipedia, the free encyclopedia 及其他互联网内容

Mercator Projection

Classifications: Conformal cylindrical.
Aliases: Wright (rare).
Available forms: Forward and inverse, spherical and elliptical projection.
Usage and options: +proj=merc +lat_ts=Φ

每个网格为 $30^\circ$，以东经 $90^\circ$ 为中心制图。

表示范围：经度 $12×30^\circ=360^\circ$，维度为 $6×30^\circ=180^\circ$，可表示整个球

数学表达：

${\begin{aligned}x&=\lambda -\lambda _{0}\\y&=\ln \left(\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right)\\&={\frac {1}{2}}\ln \left({\frac {1+\sin(\varphi )}{1-\sin(\varphi )}}\right)\\&=\sinh ^{-1}\left(\tan(\varphi )\right)\\&=\tanh ^{-1}\left(\sin(\varphi )\right)\\&=\ln \left(\tan(\varphi )+\sec(\varphi )\right).\end{aligned}}$

矩形大小：宽为 $2\pi r$ ，高为 $\infty$，

失真情况：除了赤道以外纬线圈均存在拉伸，所有经线存在拉伸。

墨卡托投影法 - 维基百科，自由的百科全书

Transverse Mercator Projection

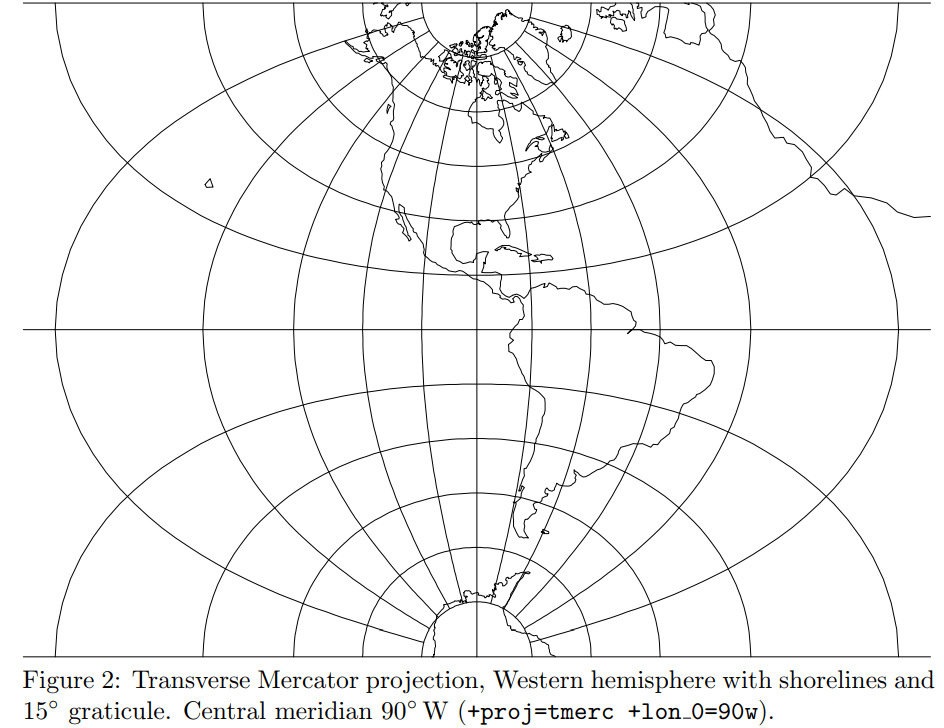
Classifications: Transverse cylindrical. Conformal.
Aliases: Gauss Conformal (ellipsoidal form), Gauss-Kruger (ellipsoidal form), Transverse Cylindrical Orthomorphic
Available forms: Forward and inverse, spherical and elliptical projection.
Usage and options: +proj=tmerc +lac_0=Φ +k=k_0

每个网格 $15^\circ$，以东经 $90^\circ$ 为中心制图。

表示范围：经度范围 $12\times 15^\circ=180^\circ$，维度范围 $12\times 15^\circ=180^\circ$，表示半个球

数学表达：

$x'=-a\lambda '\,\qquad y'={\frac {a}{2}}\ln \left[{\frac {1+\sin \varphi '}{1-\sin \varphi '}}\right].$

矩形大小：宽为 $\infty$ ，高为 $\pi r$ 。(中心的横线为半个赤道)

Transverse Mercator projection - Wikipedia

Oblique Mercator Projection

THE OBLIQUE MERCATOR PROJECTION: Empire Survey Review: Vol 13, No 101

Universal Transverse Mercator (UTM) Projection

Usage and options: +proj=utm +south +zone=zone

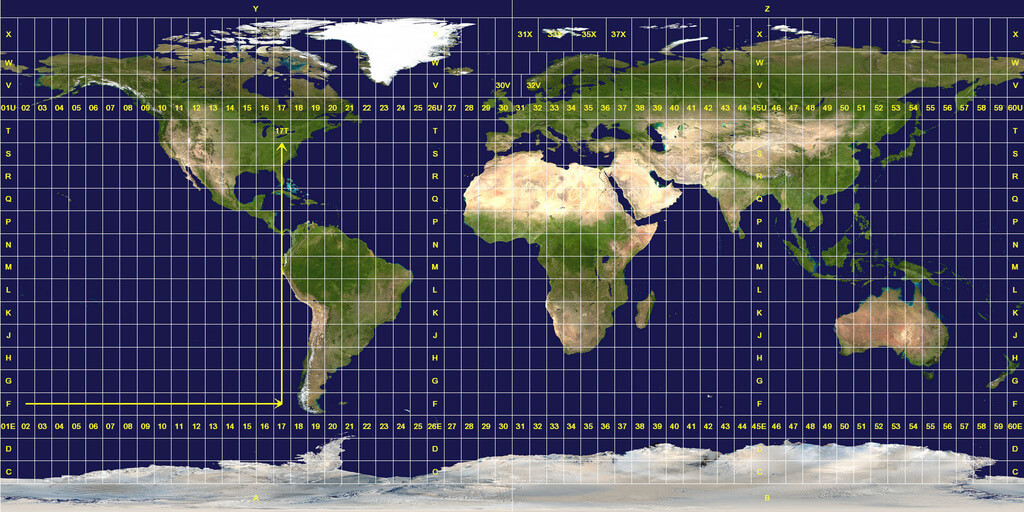
一种国际标准化的地图投影法。每 $8^\circ$ 为一个纬度区间，每 $6^\circ$ 为一个经度区间制图

表示范围：维度 $S80^\circ \sim N84^\circ $，经度 $E90^\circ \sim W90^\circ$ ，覆盖世界上大部分陆地

矩形大小：宽度 $2\pi r$ ，高度 $\frac{164^\circ}{180^\circ}\pi r=0.911\pi r$

失真情况：

从南纬80°开始，每8°被编排为一个纬度区间，而最北的纬度区间（北纬74°以北之区间）则被延伸至北纬84°，以覆盖世界上大部分陆地。

通用横轴墨卡托投影 - 维基百科，自由的百科全书

Central Cylindrical Projection

与 Mercator Projection 相似，但是不同。转换公式如下

$x = R(\lambda-\lambda_0), y = R\tan\varphi$

矩形大小：宽度 $2\pi r$ ，高度 $\infty$

失真情况：除了赤道以外纬线圈均存在拉伸，所有经线存在拉伸。可见在极点处有 $y \to \infty$ ，失真无限大。

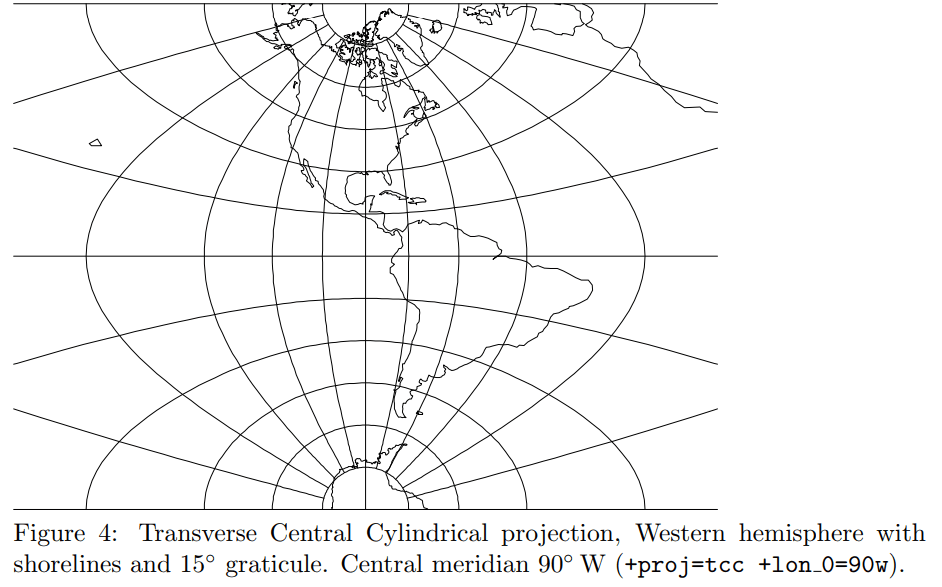
Central cylindrical projection - Wikipedia

Transverse Central Cylindrical Projection

Miller Projection

经线彼此平行且间距相等，纬线也彼此平行，但离极点越近，其间距越大，向极点靠近时，两条纬线的间距比墨卡托投影的小。两个极点均显示为直线。这样就降低了面积变形程度，但这会导致局部形状和方向发生变形。

数学表达：

$\begin{aligned} & x = \lambda \\ & y = \frac{5}{4}\ln[\tan(\frac{\pi}{4}+\frac{2\varphi}{5})] = \frac{5}{4}\sinh^{-1}(\tan\frac{4\varphi}{5}) \end{aligned}$

公式中可见，先将维度放缩 4/5，最后乘上 5/4 以保持和赤道相同的缩放比例。因此，经线长度约为赤道的0.733

矩形大小：宽为 $2\pi r$ ，高为 $2\times 0.733 \pi r = 1.466 \pi r$，

米勒圆柱投影 | 麻辣GIS
Miller cylindrical projection - Wikipedia

Lambert Cylindrical Equal Area Projection (EAP)

数学表达：

${\begin{aligned}x&=(\lambda -\lambda _{0})\cos\phi_s\\y&=\sin \varphi\sec\phi_s \end{aligned}}$

其中 $\phi_s$ 为标准纬线，上图标准纬线取了赤道。

矩形大小：宽度 $2\pi r$，高度 $2r$ ；即与球体等面积 $4\pi r^2$

失真情况：纬线除了赤道均有拉伸，所有经线有压缩

Lambert cylindrical equal-area projection - Wikipedia

根据缩放系数不同，有变形的 Gall-Peters Projection Gall–Peters projection - Wikipedia，同样是等面积映射

${\begin{aligned}x&={\frac {R\pi \lambda \cos 45^{\circ }}{180^{\circ }}}={\frac {R\pi \lambda }{180^{\circ }{\sqrt {2}}}}\\y&={\frac {R\sin \varphi }{\cos 45^{\circ }}}=R{\sqrt {2}}\sin \varphi \end{aligned}}$

Transverse Cylindrical Equal Area Projection

数学表达：

${\displaystyle {\begin{aligned} &x=\cos\phi\sin(\lambda-\lambda_0)\\ &y=\tan^{-1}\left[\frac{\tan\phi}{\cos(\lambda-\lambda_0)}\right]-\phi_0 \end{aligned}}}$

Cylindrical Equal-Area Projection — from Wolfram MathWorld

Gall (Stereographic) Projection

即非等面积，也不是保形的圆柱映射。其试图平衡映射中的失真 。

数学表示：

$x={\frac {R\lambda }{\sqrt {2}}}\,;\quad y=R\left(1+{\frac {\sqrt {2}}{2}}\right)\tan {\frac {\varphi }{2}}$

矩形大小：宽度 $\sqrt{2} \pi r$ ，高度 $(1+\frac{\sqrt 2}{2}) r$

失真情况：纬线除了赤道均有拉伸，所有经线有拉伸。

Gall stereographic projection - Wikipedia

Equidistant Cylindrical Projection (ERP)

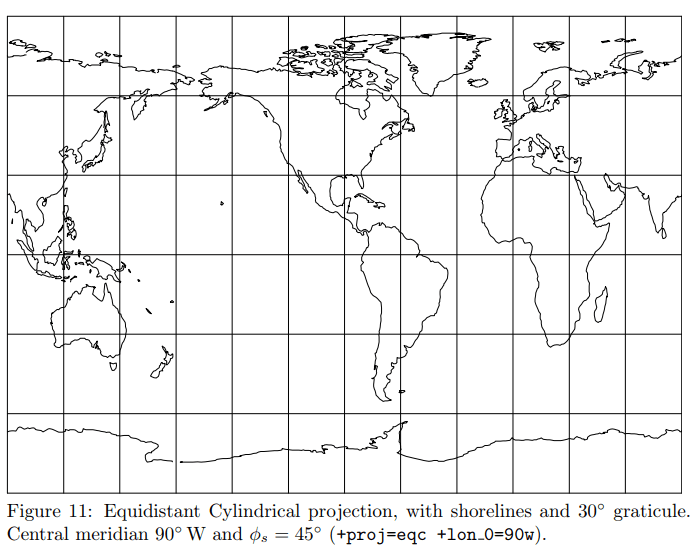
既不是等面积也不是保形的映射

数学表达：

${\begin{aligned}x&=(\lambda -\lambda _{0})\cos \varphi _{1}\\y&=(\varphi -\varphi _{1})\end{aligned}}$

$\varphi_1$ 是标准纬线，$\lambda_0$ 为图中心的经线

矩形大小：宽度 $2\pi r$ ，高度 $\pi r$ ，所以非等面积

Equirectangular projection - Wikipedia

Cassini Projection

先对球进行旋转，然后进行 ERP 投影

数学表示：

$x=\arcsin(\cos \varphi \sin \lambda )\qquad y=\arctan \left({\frac {\tan \varphi }{\cos \lambda }}\right).$

It is the transverse aspect of the equirectangular projection
Cassini projection - Wikipedia