Deep Image Prior

目前图像处理应用中使用的方法可以分为两类，基于学习的深度卷积网络 和 不需要学习的人工图像先验方法。

作者认为深度网络模型具有良好表现的原因在于

• 网络对图像先验的 学习能力 ( 从数据集中学习到图像先验，与训练方式有关 )
• 网络结构 自身对图像统计信息的 捕获能力

由此提出了一种不需要学习（训练）的深度网络模型使用方法。

网络的 泛化性 需要 网络结构 和 训练集 达到一种 “谐振” 的状态，二者的非谐振状态（注意这并非过度训练）会导致网络过拟合。即在训练集固定情况下，决定网络性能的因素除了学习外（ 这里的学习指训练方式 ），还取决于网络结构自身。

论文：Deep Image Prior

Method

通常的学习方法是，将卷积网络在训练集上迭代训练，完成对网络参数的学习。在测试时，将输入数据送入训练好的网络得到输出结果。

而本文的方法中，卷积网络直接使用随机初始化的参数值。在测试时，使用单个输入数据，进行网络参数的拟合，使得在给定任务下输出最大可能性的结果。因此决定最终结果好坏的因素只在于输入数据和网络结构 。

除了标准的图像修复任务 ( denoising \ inpainting \ super-resolution )，作者还在另外两种应用中演示了该技术

1. 将深度网络中的激活值重构为图像 ( natural pre-image )
2. Flash-no flash reconstruction

conception

将图像生成任务中使用的生成/解码网络记为 $x=f_{\theta}(z)$ ，表示将随机编码向量 $v$ 映射为一个图像 $x$ 。对应本文去噪、超分辨等任务中的 $z$ 是一个输入图像 $x_0$ ，$x$ 是输出图像，在大部分实验中作者使用了 U-Net 类型的网络结构作为映射函数 $f$ 。

denoising \ inpainting \ super-resolution 任务可以表示为最小化能量函数的问题

$$x^{\star} = \min_x E(x;x_0)+R(x)$$

其中 $E(x;x_0)$ 根据具体问题定义，$x$ 和 $x_0$ 分别为网络的输出和输入，$R(x)$ 是正则化项。正则化项通常捕获了图像的一般化先验 (a generic prior ) 信息。

作者的实验中，使用神经网络捕获的隐式先验 deep image prior 来代替 $R(x)$ ，得到如下式子

$$\begin{aligned} & \theta^{\star}=\mathop{\rm argmin}_\theta E(f_{\theta}(z);x_0)\\ & x^{\star} =f_{\theta^{\star}}(z) \end{aligned}$$

$\theta^{\star}​$ 是使用优化器对网络进行拟合后得到的最优参数，拟合的结果是使得能量项 $E​$ 最小（ 这里可见将 $R(x)​$ 设置为了 0，使用网络结构捕获的隐式先验来作为正则项 ），$x^{\star}​$ 是在得到最优参数后的输出结果。注意，编码 $z​$ 也能作为优化目标之一，但作者实验中只对模型参数 $\theta​$ 进行优化。除了特殊说明以外，$z​$ 是 32 个特征图组成的 3D 张量，特征图大小与 $x​$ 相同。

作者在基础的图像重构任务中，定义能量函数为

$$E(x,x_0)=||x-x_0||^2$$

从而将最优化问题化为

$$\min_{\theta}||f_{\theta}(z)-x_0||^2$$

作者给出了使用四种不同输入 $x_0​$ （image、image+noise、image shuffled 随机置换像素点的图像、U(0,1) noise 白噪声）时，该能量函数在梯度下降迭代中的变化，如下

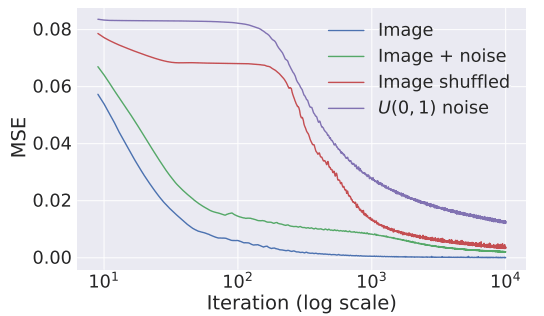
结果表示对少噪声干扰的输入，优化速度更快，而噪声多的输入，则优化速度更慢。

Application

Denoising and generic reconstruction

将噪声图像 $x_0$ 转化为清晰图像 $x$ ，作者实验中假设噪声的分布是未知的，即 blind image denoising。使用的公式为

$$\begin{aligned} & E(x,x_0)=||x-x_0||^2\\ & problem = \min_{\theta}||f_{\theta}(z)-x_0||^2 \end{aligned}$$

清晰图像为 $x^{\star} =f_{\theta^{\star}}(z)$ 。该方法未限定输入 $z$ ，因此可以直接插入任意复杂的网络后，使用复杂网络的输出作为输入。

降噪结果如下

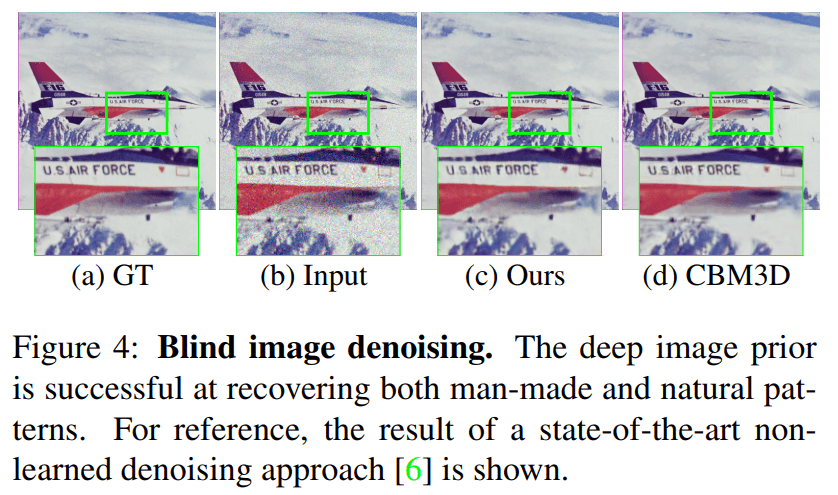
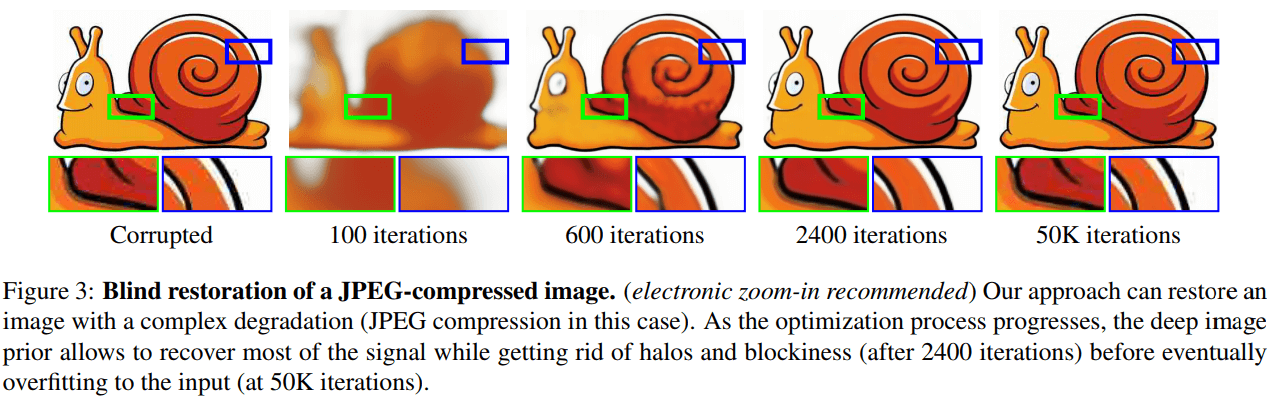
Super-resolution

输入为低分辨图像 $x_0\in \mathbb{R}^{3\times H\times W}$ 和上采样因子 $t$ ，输出为高分辨图像 $x\in\mathbb{R}^{3\times tH \times tW}$ 。设置能量函数为

$$E(x;x_0) =||d(x)-x_0||^2$$

其中 $d(\cdot):\mathbb{R}^{3\times H\times W}\to \mathbb{R}^{3\times tH \times tW}$ 为下采样操作。

从中可以看出，在超分辨任务中，使得 $E(x;x_0)$ 最小的输出结果是不唯一的，因为不同的输出结果的下采样可能相同。故需要正则化来选择最优的一个输出结果。作者依然使用网络结构捕获的隐式先验作为正则化项，所以输出为 $x=f_\theta (z)$ , 使用梯度下降优化能量函数得到参数 $\theta$ 。为每张图像设置的优化步数为 2000，得到以下结果

该方法能够达到与基于学习训练的方法类似的效果。

Inpainting

输入图像 $x_0$ 和对应的表示缺失区域的二值掩码 $m\in \{0,1\}^{H\times W}$ ，目标是重构缺失数据。能量函数定义如下

$$E(x,x_0)= ||(x-x_0)\odot m||^2$$

其中 $\odot $ 表示向量的点乘 ( Hadamard’s product ) 。

The necessity of a data prior is obvious as this energy is independent of the values of the missing pixels, which would therefore never change after initialization if the objective was optimized directly over pixel values $x$ . As before, the prior is introduced by optimizing the data term w.r.t. the reparametrization .

实验结果如下

显示该方法优于基于卷积稀疏编码的方法 ²⁵ 。

作者还进行了大块修补的实验，效果如下

对比基于学习的方法 ¹⁵

对比了不同网络结构的结果，显示越深的网络结构效果越好，而对于识别任务有效的跳跃连接结构却会使得修补效果变差。

Natural pre-image

natural pre-image method ²¹ 可以用于探究函数的不变性，如一个用于自然图像的深度学习网络的不变性。

令 $\Phi$ 表示一个神经网络的前几层，pre-image 可以表示一个图像集合 $\Phi ^{-1}(\Phi(x_0))=\{x\in\chi:\Phi(x)=\Phi(x_0)\}$ 。关于 pre-image 更详细的解释可以参考这篇文章 。

在该实验中，将神经网络的前几层作为一个函数 $\Phi$，函数输出为这几层的最后一层的激活函数输出值 $\Phi(x)$。实验输入数据为激活值 $\Phi(x_0)$ ，输出为图像 $x$ ，目标在于使得输出自然图像 $x$ 尽可能与函数 $\Phi$ 的输入自然图像 $x_0$ 相似。

作者实验中设置能量函数为

$$E(x;x_0) = ||\Phi(x)-\Phi(x_0)||^2$$

直接优化该能量函数得到的结果可能会有明显的 artifacts ，即结果不是像自然图像。需要限制输出属于自然图像集合 $\chi$ ，即 natural pre-image 。

在实验中 natural pre-image 可以通过正则化项实现，论文 ²¹ 的作者选用 TV norm 作为正则化项，本文作者使用 deep image prior ( 即网络结果捕获的图像先验 ) 作为正则化项。

实验结果如下

对比了论文 ⁸ 和 ²¹ ，deep image prior 效果明显更优。

Flash-no flash reconstruction

本实验在于单张图像修复。输入 flash image 和 no-flash image ，输出一张场景亮度和 no-flash image 相似的图像，同时使用 flash image 来减少噪声水平。

与去噪实验相同，作者将问题表示为

$$problem = \min_\theta||f_\theta(z)-x_0||^2$$

同时使用 flash image 作为输入 $z​$ 。实验结果如下

Annotation

TV norm: Total Variation Denoising

Natural pre-image: pre-image

⁸. Inverting Convolutional Networks with Convolutional Networks ↩

¹⁵. Globally and locally consistent image completion ↩

²¹. Understanding Deep Image Representations by Inverting Them ↩

²⁵. Convolutional Dictionary Learning via Local Processing ↩