PR-AUC 和 ROC-AUC 机器学习的重要评价指标,常用于二元决策问题。
Define of PR and ROC
| predicted positive | predicted negative | |
|---|---|---|
| actual positive | TP | FN |
| actual negative | FP | TN |
PR
P 为 precision,预测中的正例与所有预测之间的比值,表示正例在预测中的精度;
R 为 recall,预测中的正例与数据集中所有正例之间的比值,表示正例的查全率;
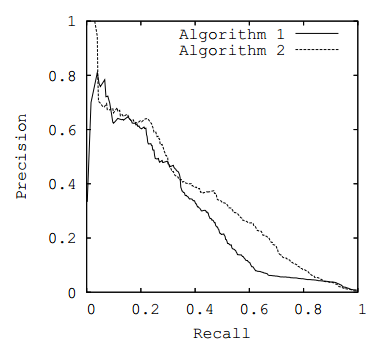
Nature of RP Curve
作 PR 图时以 P 为 y 轴,R 为 x 轴
一般 PR 曲线在 x 大于某一数值 $a$ 后,表现为减函数。因为在数据集不变且算法性能不改变情况下,要增大查全率(x 轴),需要增大预测总数量,此时所预测的反列会变多,导致正例在预测中的精度(y轴)下降
假设某算法需要达到 $a$ 的查全率时,需要的预测总数至少是 $A$ (只有预测总数增多,查全率才可能增大)
- 当预测总数小于 $A$ 时,由于预测总数较少,随着预测总数的增加,预测正例的增加 $TP_{rate}$ 大于一定的预测反例的增加 $FP_{rate}$,此时可能出现 P 增大,表现为增函数
- 当预测总数小于 $A$ 时,随着预测总数的增加,有可能因为算法性能差,预测正例的增加 $TP_{rate}$ 不大于一定的预测反例增加 $FP_{rate}$ ,导致 P 减少,表现为减函数
- 当预测总数大于 $A$ 后,随着预测总数的增加,预测正例数量 $TP$ 趋于稳定,预测反例 $FP$ 增多,导致 P 减小,表现为减函数
RP 曲线为预测正例准确度和预测正例查全率之间的映射关系,当预测总数足够大时,查全率可达到1,而此时预测反例很多,预测正例准确度趋于0,即曲线收敛于点 $(1,0)$
AUC
即 area under curve。当算法在较小的预测总数时能达到较高的查全率和正例准确度时,表示算法的性能好。此时 PR 曲线趋于右上方,即曲线的性能越好,则此时应该尽可能”右凸“,曲线下面积尽可能大。
故 PR-AUC 越大,表示算法性能越好。
ROC
TPR 为 true positive rate,预测中的正例与数据集中所有正例之间的比值,可表示正例查全率;
FPR 为 false positive rate,预测中的反例与数据集中所有反例之间的比值,表示反例的查全率;
可见 R = TPR。
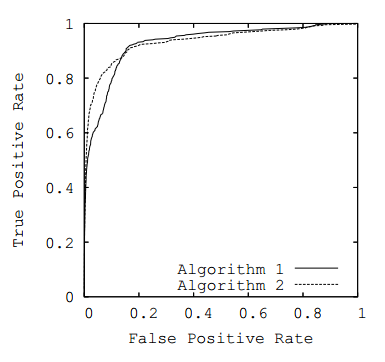
Nature of ROC Curve
作 ROC 图时以 TPR 为 y 轴,FPR 为 x 轴。在 ROC 图中作直线 $x=a$ ,该直线与某算法的 ROC 曲线焦点 $(a,y(a))$ 表达该算法在反例查全率达到 $a$ 时,能有多大的正例查全率;作水平直线同理。
一般来说,算法随着其反例查全率增大( x 增大),其正例查全率也增大( y 增大),算法的ROC曲线为增函数。因为数据集不变情况下,一般算法所预测的总数变多,预测的正例和反例都会变多
- 若预测的总数变多,而正例数不变,反例数变多,ROC 为水平,则要么是该算法已经达到较高的正例查全率(曲线位于右上方),要么表示该算法性能较差,无法提高正例查全率
- 若预测的总数变多,反例数不增多,而正例增多,表示预测总数还不足够多,未能达到算法的预测能力容量,此时曲线往往应该处于 x 较小的地方,且比较陡峭
- 随着预测总数量的变多,算法不应存在预测正例数减少或预测反列数减少的情况。
AUC
当反例查全率较小,且正例查全率较大时,算法的性能较好。此时 ROC 曲线应该趋于左上方,尽可能”左凸”,曲线下面积变大。
故 ROC-AUC 越大,表示算法性能越好。
Relationship Between PR and ROC
根据论文 The Relationship Between Precision-Recall and ROC Curves ,有以下结论:
- 对于给定 positive 和 negative 样本的数据集,若 Recall 不等于 0,则 ROC 空间和 PR 空间上存在唯一对应的两条曲线,这两条曲线也唯一确定了一个 confusion matrices
- ROC 空间上某曲线完全大于等于另一条曲线当且仅当该曲线在 PR 空间的对应曲线也完全大于等于另一条曲线(a curve dominates in ROC space if and only if it dominates in PR space)
- 一个算法优化 ROC-AUC 不等于优化了 PR-AUC
Example
已知数据集为 1000,000 份文档中,其中与关键词目标匹配的文档有 100 份。现有两个method
method 1: 检索出 100 份文档,其中有 90 份匹配正确,其余匹配错误
method 2: 检索出 2000 份文档,其中有 90 份匹配正确,其余匹配错误
PR and ROC for method 1
| predicted positive | predicted negative | |
|---|---|---|
| actual positive (100) | TP = 90 | FN = 10 |
| actual negative (999,900) | FP = 10 | TN = 999,890 |
PR for method 1:
P = 90 / (90 + 10) = 0.9
R = 90 / (90 + 10) = 0.9
ROC for method 1:
TPR = 90 / (90 + 10) =0.9
FPR = 10 / (10 + 999,980) = 0.00001
PR and ROC for method 2
| predicted positive | predicted negative | |
|---|---|---|
| actual positive (100) | TP = 90 | FN = 10 |
| actual negative (999,900) | FP = 1910 | TN = 998,080 |
PR for method 2:
P = 90 / (90 + 1910) = 0.045
R = 90 / (90 + 10) = 0.9
ROC for method 2:
TPR = 90 / (90 + 10) = 0.9
FPR = 1910 / (1910 + 998,080) = 0.00191
Compare PR and ROC
| PR | method 1 | method 2 | diff |
|---|---|---|---|
| P | 90 / (90 + 10) = 0.9 | 90 / (90 + 1910) = 0.045 | 0.855 |
| R | 90 / (90 + 10) = 0.9 | 90 / (90 + 10) = 0.9 | 0.0 |
| ROC | method 1 | method 2 | diff |
|---|---|---|---|
| TPR | 90 / (90 + 10) =0.9 | 90 / (90 + 10) = 0.9 | 0.0 |
| FPR | 10 / (10 + 999,980) = 0.00001 | 1910 / (1910 + 998,080) = 0.00191 | 0.00190 |
可见 PR 上 P 的差异大于 ROC 上 FPR 的差异。因为前者只考虑了 method 所预测的 positive (TP + FP),而后者考虑了数据集中的 negative (FP + TN),由于数据集中的 negative 很大,导致 FPR 的差异很小。
所以当数据集中的 negative 很大时(数据失衡),ROC 差异较小,PR 更能表现算法之间的差异。
Typically, if true negatives are not meaningful to the problem or negative examples just dwarf the number of positives, precision-recall is typically going to be more useful
Clearly, the PR is much better in illustrating the differences of the algorithms in the case where there are a lot more negative examples than the positive examples.