Box Convolutions

卷积操作是 CNN 中插件的基本操作，由于提取输入数据的特征。卷积类型有很多种，本次介绍 Box Convolutions

原论文: Deep Neural Networks with Box Convolutions
论文相关实现: shrubb/box-convolutions

Convolution

卷积简单的理解就是一个矩阵乘法，如图像应用中常见的 2D 卷积，以一个卷积核作为一个矩阵，和由图像像素组成的矩阵进行乘法，同时在图像的长宽两个维度上进行滑动以遍历所有像素。

卷积核的大小即是矩阵的大小（矩阵是三维 in_channel、kernel_size_h 、kernel_size_w ，其中 in_channel 由输入决定，下文讨论卷积核矩阵大小时默认指 kernel_size_h 和 kernel_size_w）。

卷积核对应矩阵的大小代表该核一次卷积操作能够提取的原始输入数据的多少，即接收域 (receptive field) 。如 3x3 卷积一次只能从该卷积输入中的 9 个像素数据中提取特征（接收域是相对的）。而矩阵的大小也代表这卷积核的参数数量，3x3 卷积核有 9 个参数（不算 bias）需要学习。

VGG 中使用了很多小卷积 (3x3) ，使用小卷积可以减少网络的参数（减少网络参数这点本身有 Regularization 的作用）。虽然小卷积的接收域小，每次提取的特征都很 “local” , 但是 VGG 模型很深，通过叠加层数，后面几层的小卷积相对原始输入的接收域变大，使得模型依然能够学到抽象特征。

Box Convolution

为了增大卷积核的接收域，有两种简单的方式，一种是直接使用大核，这会导致模型参数变多，另一种是叠加模型层数，使小卷积相对原始输入的接收域增大。还有些其他方式，如采用空洞卷积 (dilated convolution) ，对输入进行下采样等。

本次所讨论的原论文作者则提出了一种新的卷积方式，能增大卷积接收域的同时又不增加卷积层的参数，即 Box Convolution 。

Box Convolution Layer

作者给出了实现代码，从其 Git 上的 README.md 中可以知道，该卷积类似 groups=input_channels 的 conv2d ，及使用一个矩形框表示一个卷积面积，而一个矩形宽度只需要 4 个参数就可以表示，即矩形的宽度、高度和矩形左上角坐标相对输入数据中左上角坐标的位置。

接下来看看作者在论文中的描述，作者使用 $\theta=(x_{\min},x_{\max},y_{\min},y_{max})$ 来表示一个矩形的位置和大小，即在输入图像上建立坐标系，这四个参数为该坐标上的值，所以矩形大小为 $(y_{\max}-y_{\min}) \star (x_{\max}-x_{\min})$ 。

作者首先定义了一个 box averaging kernel 函数

$K_{\theta}(x,y) = \frac{ {\mathbb I}(x_{\min}\le x\le x_{\max}) {\mathbb I}(y_{\min}\le y\le y_{\max})}{(x_{\max}-x_{\min})(y_{\max}-y_{\min})}$

其中 ${\mathbb I}$ 为 indicator function （简单理解就是输入在范围输出 1 ,否则输出 0 ），$K_{\theta}$ 的分母明显是矩行面积，整个公式即表示当输入在矩形框内时输出值为 1/矩形面积，否则为 0 。

然后由于输入图像的表示是离散的（如图像的每个像素可以用整数表示坐标，但是不存在半个像素），所以作者对再引入一个函数将离散的输入表示 $\hat {\rm I}$ 转化为连续的输入表示 ${\rm I}$

${\rm I}(x,y) =\begin{cases} {\hat{\rm I}_{[x],[y]} }, & (1\le [x]\le h) \cap ( 1\le [y] \le w) \\ 0, &{\rm otherwise} \end{cases}$

然后使用一个积分操作作为卷积输出，输出表示 ${\rm O}$ 是连续的，还需要转化为离散的表示 $\hat{\rm O}$

$\begin{aligned}{\hat{\rm O} }_{x,y} = {\rm O}_{x,y } & = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}{\rm I}(x+u,y+v)K_{\theta}(u,v){\rm d}u{\rm d}v \\ & = \frac{1}{(x_{\max}-x_{\min})(y_{\max}-y_{\min})}\int_{x+x_{\min} }^{x+x_{\max} }\int_{y+y_{\min} }^{y+y_{\max} } {\rm I}(u,v){\rm d}u{\rm d}v \end{aligned}$

二维上的积分表示面积，${\rm I}$ 的返回值是 1 或 0 ，而 $K_{\theta}$ 包含一个面积参数作为分母，从而使得 ${\rm I}$ 和 $K_{\theta}$ 乘积的积分可以表示矩形框内像素数据的求和

有了卷积公式，就可以得到分别对输入和参数求导计算梯度。论文中还描述了卷积的一些细节，如矩形大小和位置的随机初始化，以卷积参数更新时 $x_{\max}\ge x_{\min}$ 和 $y_{\max}\ge y_{\min}$ 的约束，在实现时将积分运算转化为像素值求和，即加法运算。

Embedding box convolutions into an architecture

作者给出了一个含有 Box Convolutions 的层结构，如图

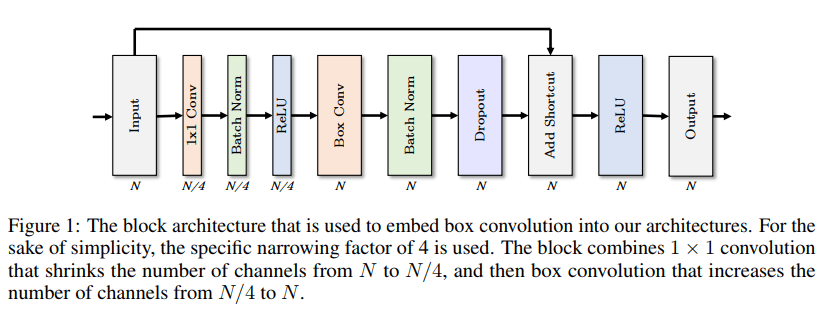
包含了 1x1 卷积和其他操作。现在来讨论下该结构的 计算量 和 参数量 。

普通的 conv2d 的参数量是 $in\_channel \star kernel\_size\_h \star kernel\_size\_w * out\_channel + out\_channel$ 。

而 Box Convolution 类似 groups=in_channel 的 conv2d ，即一个卷积核对应每个输入 feature 都有一个卷积（矩形），且一个卷积核输出 in_channel 个 feature ，所以一个卷积核有 $4\star in\_channel$ 个参数，n 个卷积核则有 $4\star in\_channel\star n$ 个参数（对应论文中的 $4NM$ 个参数的描述）。

使用作者的实现进行验证的结果如下

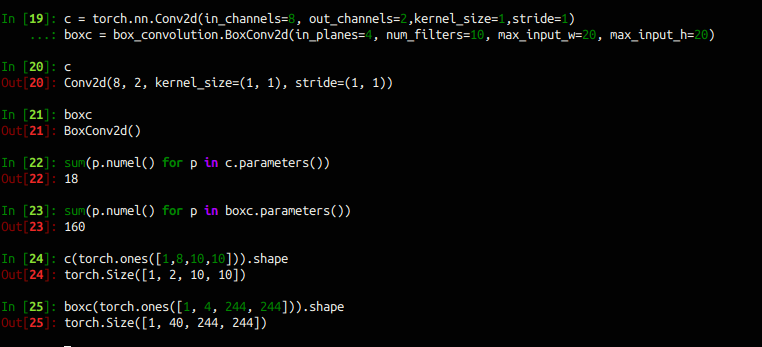
可见 conv2d 的参数量有算 bias ，而 box convolution 没有 bias ，并且在 conv2d 使用 out_channels 设置输出通道数， 而box convolution 的输出通道数为 $in\_planes \star num\_filters$ 。

回到论文给的那个层结构，输入数据通道数 N ， 1x1 Conv 输出通道为 1/N ，所以参数为 $N^2+N$ ，而 Box Conv 输入通道 N/4 ，输出通道数N，所以这里是卷积核数量 $num\_filters=\frac{out\_planes}{in\_planes} = \frac{N}{N/4} = 4$ ，Box Conv 参数总量为 $4\star 4 \star N = 16 N$ 。对应论文中的描述 $O(N^2)$ 和 $O(N)$ 。

可见在使用 Box Conv 时，当输出通道确定后，其参数总量就确定了。而在输入通道不能整除输出通道时，需要使用 1x1 Conv2d 修改输入通道数。单纯使用 Box Conv 只能增加或者不修改输入通道数。

Experiments

为了验证 Box Convolution 的效果，作者使用图像的语义分割任务。使用 ENet 和 ERFNet 作为 baseline，替换 baseline 中的几个残差块为上一节中层结构，构造新的模型。为了评价 Box Convolution ，作者还设计了该卷积重要性的计算方式。验证效果如下

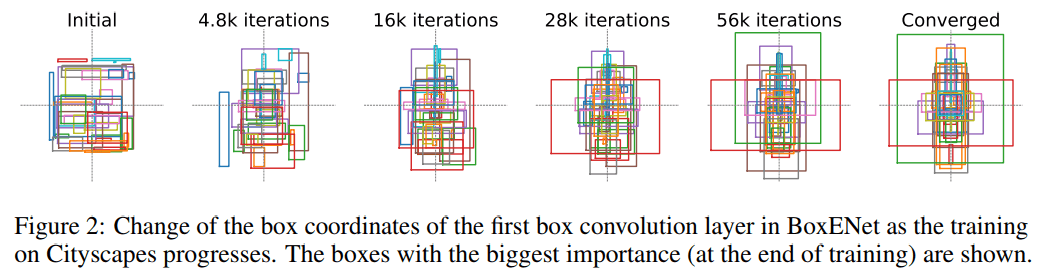
在模型收敛后，观察到 Box 出现垂直对称趋势，如上图。作者认为这可能可以将 Box 的表示由四个参数改为三个参数，即水平位置（宽度）只需要一个参数就可以表示。

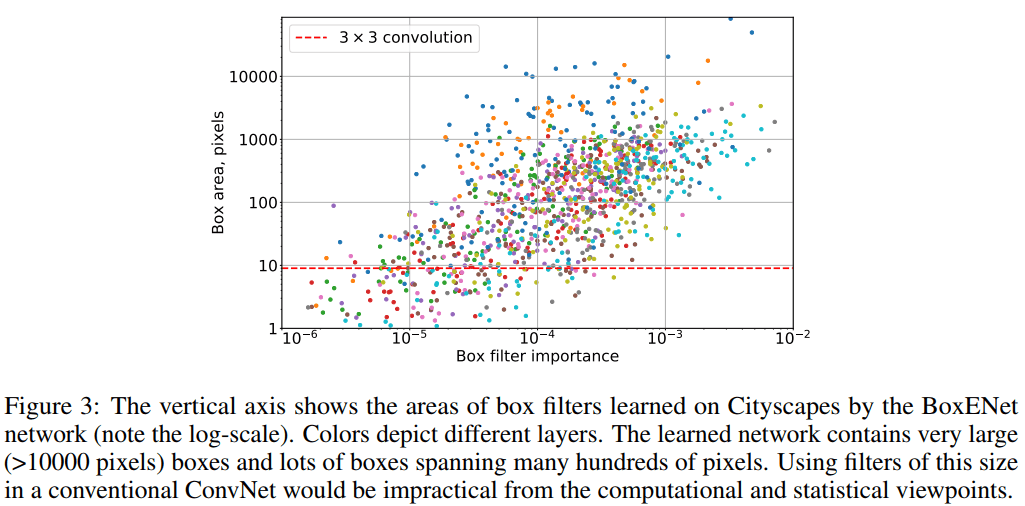
作者还统计了 Box 的尺寸和其重要性的关系，如上图，表示有很多 Box 都具有很大的面积，且其重要性很高。作者认为这表示网络在很大程度上依赖与大尺寸的卷积核。而标准的卷积方式难以达到大核效果（标准大核参数多，容易过拟合，且难以训练）。