本文使用 attention 机制 结合 RNN 处理 视觉问题。
显著性检测只基于低水平的图像信息(低水平的图像特征对比),忽略了图像内容的语义信息和任务需求。
The Recurrent Attention Model (RAM)
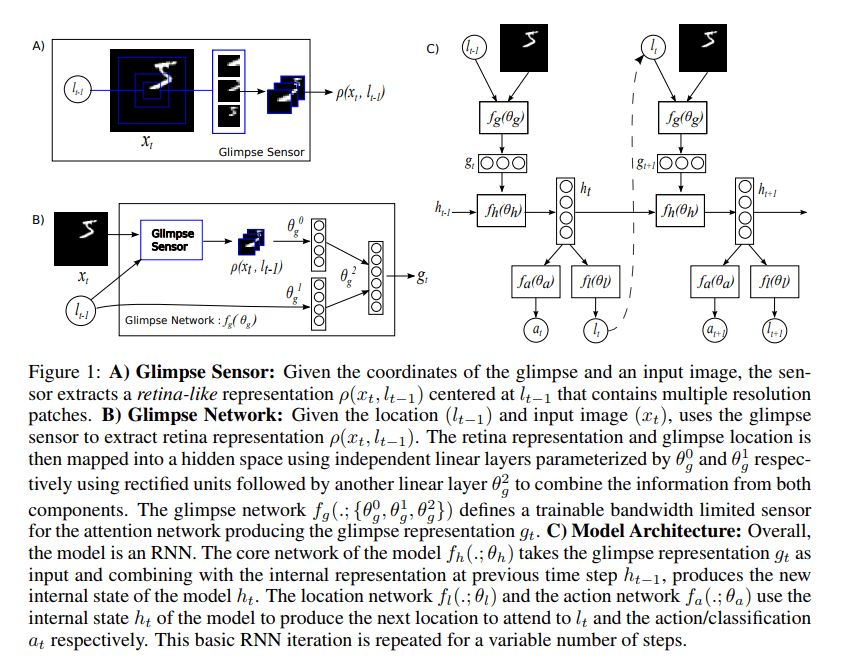
Model
模型使用了 RNN 结构。
Sensor:在每一步$t$,对于输入图像 $x_t$ ,sensor 可以获取其中位于 $l_{t-1}$ 的 retina-like 表示 $\rho(x_t,l_{t-1})$ ,该表示的大小小于输入图像大小,表示一个注意范围。sensor 使用高分辨率编码 $l$ 周围的区域,并且逐步降低分辨率来编码远离 $l$ 的像素,从而生产一个维度小于 $x$ 的向量。这种编码方式参考了 glimpse 14 ,是Figure 1 中的 B。使用 glimpse 网络 $f_g$ 生成特征向量 $g_t=f_g(x_t,l_{t-1};\theta_g)$ ,其中 $\theta_g=\{\theta_g^0,\theta_g^1,\theta_g^2\}$ 。
Internal state:模型中的 internal state 为过去观察到的状态信息的总和,指导 action 的决策和 sensor 的放置。该 internal state 由 RNN 的隐藏单元 $h_t$ 表示,并且由核心网络逐时间步更新 $h_t=f_h(h_{t-1},g_t;\theta_h)$ 。
Actions:每一时间步上,网络有两类型的 actions 。一是位置 action,使用 $l_t$ 更新 sensor 位置;二是环境 action $a_t$,这能够影响改变环境状态,其依赖于具体任务。本文中位置 action 是从位置网络 $f_l(h_t;\theta_l)$ 生成的分布中随机选取一个位置;环境 action 是从动作网络 $f_a$ 的输出中进行操作 $a_t\sim p(\cdot|f_a(h_t;\theta_a))$ 。模型也可以额外添加 action 用于决定何时停止 glimpse 。
Reward:执行 actions 后将得到新的环境的视觉观测状态 $x_{t+1}$ (新的输入)和一个奖励信号 $r_{t+1}$ ,模型目标是最大化奖励 $R=\sum_{t=1}^T r_t$ 。在分类问题上,执行 $T$ 步后若分类正确则 $r_T = 1$ ,否则为 0 。
Training
需要训练的参数有 glimpse 网络参数、core 网络参数和 action 网络参数 $\theta=\{\theta_g,\theta_h,\theta_a\}$ 。
学习的策略包含一个交互序列 $s_{1:N}$ 之上的分布,目标是在该分布下最大化奖励 $J(\theta) = E_{p(s_{1:N};\theta)}[\sum_{t-1}^T r_t] = E_{p(s_{1:N};\theta)} [R] $ ,其中 $p(s_{1:N};\theta)$ 依赖于策略。
最大化 $J$ 的问题可以视为 RL 中的一个 POMDP ,并且可以的到其近似导数26 :
其中 $s^i$ 是执行策略 $\pi_{\theta}$ 后的交互序列,$i=1…M$ 为 episodes 。
该等式需要计算 $\nabla_{\theta}\log \pi(u_t^i|s^i_{1:t};\theta)$ ,这是 RNN 在时间步 $t$ 的梯度。
Variance Reduction:修改导数为如下形式以减小方差
其中 $R_t^i=\sum_{t’=1}^Tr_{t’}^i$ 为执行 action $u_t^i$ 后的累计奖励,$b_i$ 是依赖于 $s^i_{1:t}$ (via $h_t^i$ ) 的 baseline ,根据强化学习文献,选择取值为 $b_t=E_{\pi}[R_t]$ 21。
Using a Hybrid Supervised Loss:上诉描述在 the “best” actions 未知且只有 reward 为学习信号的情况下训练模型。某些情况下,执行 action 后的正确性是可知的。如对象检测任务中,最后 action 是给出一个对象的 label,在监督模型下,对象 label 是已知的,可以直接优化策略以输出正确的标签。即优化条件概率 $\log\pi(a_{T}^{\star}|s_{1:T};\theta)$ ,其中 $a^{\star}_{T}$ 对应于观察序列 $s_{1:T}$ 下图像的 ground-truth label 。由此可以使用交叉熵损失函数来训练 action network ,并方向传播到 core network 和 glimpse network,只有 location network $f_l$ 需要使用强化学习。
Experiment
实验的通用设计:
Retina and location encoding:retina encoding $\rho(x,l)$ 抽取 $k$ 个以 $l$ 为中心的方形块, 第一块大小为 $g_w\times g_w$ 像素,后续的每块宽度为上一块的两倍;然后 $k$ 个块再 resize 到 $g_w\times g_w$ 大小。Glimpse location $l$ 是实数对 $(x,y)$ ,其坐标系原点 $(0,0)$ 为图像 $x$ 的中心,且 $(-1,-1)$ 为图像的左上角。
Glimpse network: Glimpse network $f_g(x,l)$ 具有两个全连接层。使用 $Linear(x)=Wx+b$ 作为向量 $x$ 的线性变换,使用 $Rect(x)=max(x,0)$ 为非线性整流。该网络的输出为
其中 $h_g$ 和 $h_l$ 维度为 128,$g$ 维度为 256。
Location network:位置 $l$ 的策略由具有固定方差的双分量高斯定义。在时间 $t$ 上,位置网络输出位置策略的均值,其定义为 $f_l(h) =Linear(h)$ ,其中 $h$ 是核心网络/RNN 的状态。
Core network: 对于分类实验,核心 $f_h$ 是一个整流单元,定义为 $h_t =f_h(h_{t-1}) =Rect(Linear(h_{t-1})+Linear(g_t))$ 。动态环境下的实验(the experiment done on a dynamic environment )使用了 LSTM 单元。
Image Classification
分类决策在最后一个时间步给出 $t=N$ 。action network $f_a$ 为线性 softmax 分类器 $f_a(h)=\exp(Linear(h))/Z$ ,$Z$ 为标准化常数。RNN 状态向量 $h$ 维度 256。所有方法采用随机梯度下降方式训练,minibatches 大小 20,momentum 为 0.9。学习率从初始值降为0。最后时间步上分类正确奖励 1 否则为 0,其他时间步的奖励均为 0 。
Centered Digits: 首先使用 MNIST 数字数据集做分类,验证训练方法学习 glimpse 策略的能力。retina patches 的大小设置为 $8\times 8$ ,使用 7 个 glimpses。使用标准前向反馈和卷积神经网络做比较。结果表示,随着 glimpses 的增加,本模型准确度能超过 FNN 和 CNN ,表示本模型可以成功学习并且组合多个 glimpses 的信息。
Non-Centered Digits: 先制作 Translated MNIST 数据集,这是将 MNIST 数据集图像按随机位置放到一个 $60\times 60$ 大小的空白图像上得到的。结果表示,使用 4 个 glimpses 就可以使效果比 FNN 和 CNN 好,表示该 attention 模型能够在大图像上成功搜索一个对象,无论对象是否位于图像中心。
Cluttered Non-Centered Digits:首先制作 Cluttered Translated MNIST 数据集,这是在 Translated MNIST 的基础上,随机放置 4 个 $8\times 8$ 大小的 MNIST 图像子块得到的。实验目的是验证 attention 模型在杂乱表示下关注相关部分的能力。实验结果显示,attention 模型相对另外的模型其准确度明显要好,并且对比了使用均匀放置 8 个 glimpses 模型(即同样使用 glimpses ,但是没有 attention 机制),结果证明了 attention 机制的有效性。
本文还进一步使用 8 个随机放置子块和 $100\times 100$ 的空白背景制作数据集来验证。模型的改善效果相似。并且随着图像变大,attention 模型的计算量没有改变,而 CNN 的隐藏层计算量却随着像素增加而增加。
Dynamic Environments
测试模型在动态视觉环境下学习控制策略的能力。训练模型来玩一个简单的游戏。游戏在 $24\times 24$ 像素大小的屏幕下进行,涉及两个对象,一个像素大小的球自上而下降落,底部有一个两像素大小的板。模型控制板左右移动来接住随机下落的球。接到球得到1个奖励,落空没有奖励并且游戏重新开始。
网络使用三个不同缩放后 $6\times 6$ 像素大小的 retina 区域作为输入。action network 具有三种游戏动作(左、右、不变),使用线性 softmax 模拟游戏动作分布。核心网络使用了 256 个 LSTM 单元。
结果显示模型学会了玩这个游戏,证明该模型具有学习特定任务的有效关注策略的能力。
Discussion
- 参数数量和模型计算量可以独立于输入图像大小
- 模型能够忽略图像中的 clutter present,并且关注相关的区域
- 模型灵活易于扩展
14. Learning to combine foveal glimpses with a third-order Boltzmann machine ↩
21. Policy gradient methods for reinforcement learning with function approximation ↩
26. Simple statistical gradient-following algorithms for connectionist reinforcement learning | SpringerLink ↩